|
|
| |||||||||||||
|
|
Free Boundary ProblemsSpacio-temporal behaviour of complex systems
Free boundary problems (FBP) constitute (mathematical, biological, physical, etc.) research subject characterized by the occurence of frontiers whose locations are a priori unknown. These boundaries separate geometric regions with different properties. FBP arise mainly in boundary value problems of partial differencial equations. One of the possible strategies to understand spatio-temporal complexity is to investigate simple model equations resulting in chaotic or turbulent-like patterns. The point is that the Navier-Stokes equations describing the flow of viscous fluids are far too complicated to allow detailed analytic or even numerical studies in the relevant parameter regions. To investigate mechanisms and demonstrate the birth of complicated motion in space (x) and time (t) several nonlinear partial differential equations have been suggested including the complex Ginsburg-Landau or the Kuramoto-Sivanshinsky equations. We consider perharps the simplest family of deterministic partial differential equations (PDE) with singular terms (Zhang equations). Depending on a parameter, it exhibits a behaviour which is an interesting mixture of stochastic and deterministic regimes.
The problem comes from the theory of complex directed polimers. We investigate the equation mathematically (existence, regularity, special solutions, etc.) and numerically. We found that the structures computed numerically behave locally as our special solutions. Partners Biological Physics Dep., ELTE For more information please contact Róbert Kersner and Zsolt Biró. Room K427 | |||||||||||||
  | ||||||||||||||

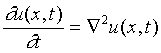 + parameter x nonlin. sing.term, e.g. pl.
+ parameter x nonlin. sing.term, e.g. pl.