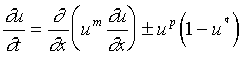|
|
| |||||||||||||
|
|
Free Boundary Problemsin Ecology and Bioscience
Free boundary problems (FBP) constitute (mathematical, biological, physical, etc.) research subject characterized by the occurence of frontiers whose locations are a priori unknown. These boundaries separate geometric regions with different properties. FBP arise mainly in boundary value problems of partial differencial equations. "The increasing study of realistic mathematical models in ecology is a reflection of their use in helping to understand the dynamic processes involded in such areas as predator-prey and competition interaction, renewable resource management, evolution of pesticid resistant strains, ecological control of pests, multi-species societies, plant-herbivore systems and so on." (Murray, J. D., 1989.) A model we are dealing with is special case of the general reaction-diffusion or the interacting population-diffusion models:
where u(x,t) is the density of the population, m, p and q are positive parameters. The curve on (x, t) plane dividing the domains where u > 0 and u = 0 (no population) is the free boundary. Our result shows the dependence of u(x, t) and the free boundary on system parameters m, p and q. Kolmogorov-Petrowski-Piscunov type resutls were also obtained on convergence in form and speed to special travelling wave.
Partners University of Tel-Aviv
For more information please contact Róbert Kersner and Zsolt Biró. Room K427 | |||||||||||||
  | ||||||||||||||