Free Boundary Problems
Lubrication approximation in the viscous film theory
and the k-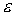 system in turbulence theory
Free boundary problems (FBP) constitute
(mathematical, biological, physical, etc.) research subject characterized by the occurence
of frontiers whose locations are a priori unknown. These boundaries separate geometric
regions with different properties. FBP arise mainly in boundary value problems of partial
differencial equations.
1./ The so-called k - 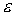system
can be derived from the exact transport equation for the Reynolds stresses by using some
closing approximations. The simplest version modeling the evolution of turbulent bursts is
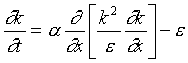
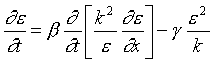
where k(x, t) in the turbulent energy
density, e (x, t) is dissipation rate of turbulent energy,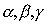 
are positive dimensionless constants.
The free boundary is the geometric boundary of the
turbulent domain, where k and e vanish. For different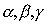
we have very different kinds of evolution.
2./ The lubrication approximation for a thin film of
liquid on a solid surface yields a fourth order degenerate diffusion equation for the film
height h.
 .
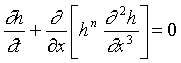Numerical calculations and matched asymptotics lead
to results which suggest a very rich structure of solutions. We study the existence of
free boundaries, their behaviour and provide different energy estimates h, and
their dependence on the parameter n.
Partners
University of Rome II
Donetsk University
University of Bath, UK
For more information please contact
Róbert Kersner and Zsolt Biró. Room K427
Laboratory of Applied Mathematics
Group of Mathematical Physics
e-mail: kersner@sztaki.hu
biro@luna.aszi.sztaki.hu
| 
