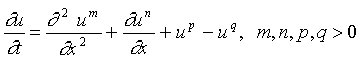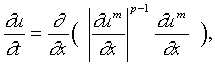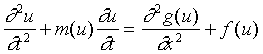|
|
| |||||||||||||
|
|
Free Boundary Problems Travelling waves in nonlinear diffusion-advection-reaction, transmission lines and in branching random walk
Free boundary problems (FBP) constitute (mathematical, biological, physical, etc.) research subject characterized by the occurence of frontiers whose locations are a priori unknown. These boundaries separate geometric regions with different properties. FBP arise mainly in boundary value problems of partial differencial equations. A travelling wave (TW) is a function of the form u = u(x - ct), c is the speed. It is called finite if u = 0 for x - ct ³ x0. Some examples of models (equations):
(porous media equation with convection, sources or sinks).
(non-Newtonian fluids in turbulent regime)
(generalized telegraph equation, correlated random walk equation) In a given model a free boundary exists if and only if the equation, has a finite travelling ware solution. The search of these solutions can be reduced to the study of a singular nonlinear integral equation whose solutions must satisfy certain constraints. Partners University of Rome 1 For more information please contact Róbert Kersner and Zsolt Biró. Room K427 | |||||||||||||
  | ||||||||||||||