4. Domain of copositivity of a parametral matrix

For the discussion of this section A(h) will denote a real parametral matrix, having the properties, we specify in the following definition.

Definition 4.1. A real parametral matrix is proper parametral matrix, if it has the following features:

(i) A(h) is symmetric for every real h.

(ii) A(h) is a continuous function of h.

(iii) For any principal submatrix B(h) of A(h) it is true that if is CP and , then is also CP.

(iv) There exists some such that A(h) is NCP.

The next statement contains examples for proper parametral matrices.

Statement 4.2. If A is a real symmetric matrix and U is a real nonzero matrix, then is a proper parametral matrix. As a special case, for a nonzero r-vector u, is a proper parametral matrix.

Proof. The validity of (i) and (ii) is obvious. If , then is positive semidefinite, therefore its principal submatrices are all CP. The sum of two CP matrices is also CP. This way, feature (iii) is established.

For the proof of feature (iv) it is enough to show that h may assume such values, for which A(h) has a negative entry in its main diagonal. Indeed, let be a nonzero row vector of U, then holds for any such h for which .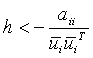

Definition 4.3. The domain of copositivity of a proper parametral matrix A(h) is the set

(4.1)           .

Definition 4.4. The threshold number of copositivity (briefly threshold) of a proper parametral matrix A(h) is the number

(4.2)           .

Remark 4.5. Because of the assumption involved in feature (iv) of Definition 4.1, only the following two possibilities may occur:

a) G is empty, and then ;

b) G is nonempty closed convex set, and then is finite. Further, in this case .