3. The Sherman-Morrison formula and related topics
Throughout this whole section, let A, B denote real or complex ![]() matrices, u, v denote r-vectors, U, V denote
matrices, u, v denote r-vectors, U, V denote ![]() matrices,
matrices, ![]() denote the unit matrix of order r, and h denote an arbitrary real or complex number.
denote the unit matrix of order r, and h denote an arbitrary real or complex number.
The Sherman-Morrison formula applies to inverting the modification of a given matrix with a dyad. If not a single dyad, but a finite sum of dyads (i.e. a matrix-product ![]() ) is added to A, then the Sherman-Morrison-Woodbury formula is applicable as a more general matrix equality. Further, it is not very difficult to give similar formulas for determinants rather than inverses, which we shall call „the Sherman-Morrison formula for the determinant", and the „Sherman-Morrison-Woodbury formula for the determinant".
) is added to A, then the Sherman-Morrison-Woodbury formula is applicable as a more general matrix equality. Further, it is not very difficult to give similar formulas for determinants rather than inverses, which we shall call „the Sherman-Morrison formula for the determinant", and the „Sherman-Morrison-Woodbury formula for the determinant".
Statement 3.1 (Sherman-Morrison formula). If A is invertible and ![]() , then
, then
(3.1) 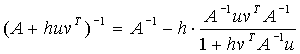 .
.
We shall prove a more general formula that will occur in the next statement.
Statement 3.2 (Sherman-Morrison-Woodbury formula). If A and ![]() are invertible, then
are invertible, then
(3.2) ![]() .
.
Proof.
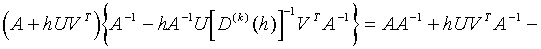
![]()
![]()
![]() .
.
Statement 3.3. For arbitrary square matrices A and B,
(3.3) 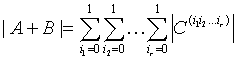 ,
,
where the j-th column of ![]() is defined by
is defined by
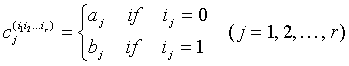 .
.
We omit the proof, which is elementary and is known from the determinant calculus.
Statement 3.4. If rank![]() , then
, then
(3.4) 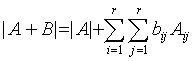 .
.
Proof. Let us consider the matrices ![]() introduced in the previous statement. If
introduced in the previous statement. If ![]() then
then ![]() contains at least two columns selected from B, and therefore the assumption about the rank of B implies that
contains at least two columns selected from B, and therefore the assumption about the rank of B implies that
![]() .
.
If ![]() and
and ![]() for
for ![]() , then
, then
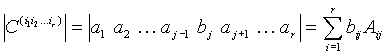
according to the determinant expansion theorem. Now we can write
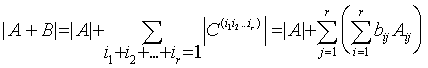 .
.
Corollary 3.5 (Sherman-Morrison formula for the determinant).
(3.5) ![]() .
.
Proof. The dyad ![]() is an
is an ![]() matrix with rank equal to 1. According to Statement 3.4, we have
matrix with rank equal to 1. According to Statement 3.4, we have
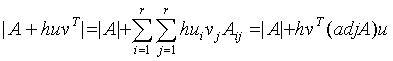 .
.
Corollary 3.6. If A is invertible, then
(3.6) ![]() .
.
The proof is obvious, if we take into account that ![]() .
.
Corollary 3.7. If A and ![]() are invertible, then
are invertible, then
![]() .
.
The proof is evident from (3.6).
For the more general case, where the vectors u and v are replaced by the matrices U and V, statements, parallel to Corollaries 3.6-3.7 will also be formulated. Before doing this, we state the following lemma, which will help us to prove the generalization of Corollary 3.6.
Lemma 3.8. Let ![]() denote a real or complex
denote a real or complex ![]() matrix, and denote
matrix, and denote
![]()
the leading principal submatrices of D. Then we state the following:
(3.7) 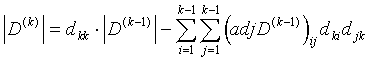 .
.
Proof. Expand the determinant ![]() according to its last row, and then expand the given smaller determinants - with the exception of
according to its last row, and then expand the given smaller determinants - with the exception of ![]() - according to their last columns. Then we obtain the sum standing on the right hand side of (3.7).
- according to their last columns. Then we obtain the sum standing on the right hand side of (3.7).
Theorem 3.9 (Sherman-Morrison-Woodbury formula for the determinant). If A is invertible, then
(3.8) ![]() ,
,
where
(3.9) ![]() .
.
Proof. We prove the theorem by induction on k. If k = 1, then the assertion reduces to the statement of Corollary 3.6.
Consider the modified matrix ![]() in the form
in the form
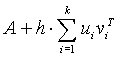
where ![]() and
and ![]() are r-vectors, and assume that the assertion of the theorem is true for k = 1, i.e.
are r-vectors, and assume that the assertion of the theorem is true for k = 1, i.e.
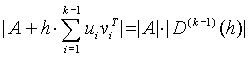 .
.
We suppose temporarily, that ![]() is invertible. Then, according to Corollary 3.6,
is invertible. Then, according to Corollary 3.6,
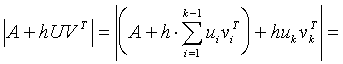
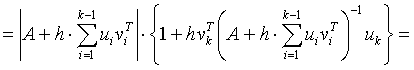
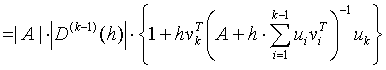 .
.
According to Statement 3.2 we can obtain, that
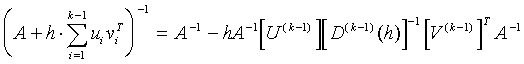
where
![]()
and similarly
![]() .
.
Thus
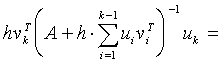
![]()
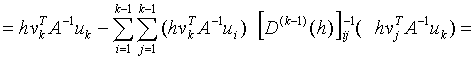
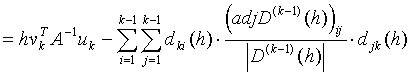 .
.
Now we can write
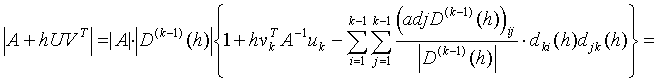
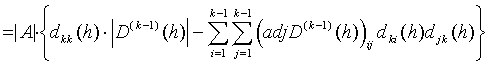 .
.
Finally, by applying Lemma 3.8 for ![]() , we obtain that (3.8) is valid, provided that
, we obtain that (3.8) is valid, provided that ![]() is invertible. As clearly
is invertible. As clearly ![]() , we can conclude that (3.8) is valid, if h is in a neighbourhood of zero. Since the expression
, we can conclude that (3.8) is valid, if h is in a neighbourhood of zero. Since the expression
![]()
is a polynomial, i.e. analytical function of h, thus if it vanishes in a neighbourhood of zero, then it does so for any complex h. By this the proof is complete.
Corollary 3.10. If both A and ![]() are invertible, then
are invertible, then ![]() is invertible as well.
is invertible as well.
Remark 3.11. The assertions of Statement 3.2 and Corollary 3.10 can be united in the following way: Suppose that A is invertible. In this case ![]() is invertible if and only if
is invertible if and only if ![]() is invertible, and then
is invertible, and then
![]() .
.
The Sherman-Morrison-Woodbury formula is cited in this form in [11], where ![]() is assumed. As we have seen, the restriction
is assumed. As we have seen, the restriction ![]() is not necessary to suppose.
is not necessary to suppose.