 APPLIED MATHEMATICS LABORATORY
APPLIED MATHEMATICS LABORATORY
STOCHASTIC SYSTEMS RESEARCH GROUP
Head: László Gerencsér
Financial mathematics
(E. Berlinger, L.Carassus, L.
Gerencsér, L. Györfi, Z. Mátyás, Gy. Michaletzky, G. Molnár-Sáska,
G. Morvai, Zs. Orlovits, M. Rásonyi, J. Száz, L. Stettner, Cs. Szepesvári, Zs. Vágó)
Arbitrage and large markets: In the theory of large financial markets it is
widely believed that there exist pricing measures exactly when there is no
arbitrage in an appropriate, asymptotic sense. Such a result has been obtained
in [40] for a class of models well-known in economic theory. An overview of
recent results on large financial markets (including those of the author) is
presented in [6*].
Applications of control theory to finance : The existence of optimal portfolio strategies and related risk-neutral pricing operators has been established in [39] and [5*] in cooperation with Lukasz Stettner (IMPAN, Warsaw Mathematical Institute of the Polish Academy of Sciences). In cooperation with Laurence Carassus (Université Paris 7) M. Rásonyi proved the continuity of optimal strategies with respect to investors’ preference relations. These results are based on those of [5*]. It has been conjectured that as risk-aversion of agents tends to infinity their respective utility prices (assigned to a contingent claim) tend to the superreplication (risk-free) price of the given claim. Up to now only very special cases of this conjecture have been shown. A further result of the above collaboration is a proof of this conjecture in a fairly general setting. These collaboration have been partly financed by the EU Centre of Excellence programme.
Behavioral finance : A stochastic feedback model for financial markets was proposed [22], in which the agent's decision is based on his beliefs of the price dynamics and his behavior reflecting his attitude, such as risk aversion or risk preference. A variety of behaviors of economic players is described by experimental psychologists, see for example the famous 1986 paper of Kahnemann and Tversky [35]. When a new agent enters the market, his/her anticipations and actions alter the market dynamics and a genuinely closed loop system arises. The market is in equilibrium if the agent’s beliefs no longer change the market dynamics. A data driven real-time procedure to find the equilibrium price predictor has been developed. The convergence of the resulting stochastic approximation procedure was analyzed using the techniques developed by Benveniste, Metivier and Priouret in [4], see also [20], and the conditions for convergence have been verified. Simulation results for various behaviors such as rational behavior, loss aversion and risk-seeking behavior were also presented. Using market dynamics fitted to real data and simple AR predictors, quick convergence of the parameter processes was established in all of our test examples.
The single-agent model was extended to a
comprehensive multi-player stock market model [21]. In this case the market dynamics is completely determined by stock
market regulations (for the currently used rules at the Budapest Stock Exchange
see [11] ) and the transaction requests of the agents.
Bid prices emerged as a new and essential element of the behavior. Various
sources of randomness were considered such as threshold dependent actions,
random bid prices and exogenous white noise. Initial experiments for the
computation of the optimal growth rates belonging to two different behaviors
(rational behavior and loss aversion) have been carried out. As preliminary findings
we noted that the wealth processes of non-rational players admit much higher
variability than those of rational players.
Stochastic volatility
models for financial time series :
The log-returns of a stock exhibits a
so-called volatility clustering phenomena: long periods of low
volatility are followed by short periods of high volatility. A typical figure
for log-returns is given in the following Figure, an SP 500 daily data for 4
years (1997-2001):
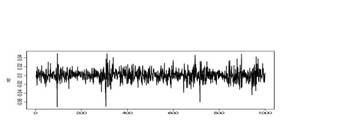
It follows that the
conditional variance is time-varying, a fact not true for linear processes. The
first basic non-linear stochastic volatility model, due to R. Engle, is the
so-called ARCH process, in which volatility is modeled by a stochastic
non-linear feedback system driven by observed log-returns. A useful
extension is the GARCH model (see [10]). GARCH processes have been applied also
for estimating the volatility of index returns, see [38], and for modelling the
joint dynamics of futures contracts, see [12]. Alternative models have can be
obtained by using bilinear stochastic systems, see [44].
A key problem is the
estimation of the parameters of a GARCH model. Strong
consistency of the quasi log-likelihood function have been established under
very weak conditions by Berkes et al., see [5]. We have taken a
different route: by assuming stronger conditions on the driving noise and
extending the techniques for ARMA processes (see [27, 28]), we have derived
strong approximation results both for the standard quasi-maximum-likelihood
estimator and also for its fixed gain version.
A basic problem is to detect structural changes in the market, which is reflected in changes of the GARCH parameters. There are several methods for detecting these changes such as hypothesis testing (see [6]), or asymptotic and bootstrap tests (see [32]). A change point detection method for GARCH processes inspired by the results of [26] and [2], leading a kind of Hinkley detector with appropriately defined residuals has been developed in [23].
Student loan systems: A stochastic model for the Hungarian student loan
system has been developed [7]. The creditor's risk was investigated in terms of
the two basic control parameters of the model, the risk premium and the
repayment quotient. Special features of the Hungarian system, such as
self-financing and writing off the debt at retirement, were also incorporated
into the model. The dependence of the creditor’s profit and the borrower’s
welfare on basic intervention parameters was analyzed using a number of
simulation examples. The findings allow for a reasonable choice of parameters
which makes the system sustainable for the lender and attractive for the
borrower. A typical debt profile is given on the figure:
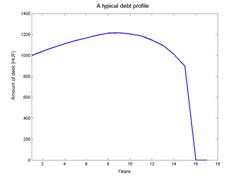
Logoptimal portfolios: Logoptimal portfolios, ensuring the maximal growth rate of the wealth
process, with transaction costs, an extension of the basic model of [13], have
been studied. This has led us to a hard
MDP (Markov Decision Process) problem. A direct approach would be to develop on-line data driven procedures, see [42], and also [34].
This has led to the sub-problem of estimating the conditional expectation of
any day’s return given the past. It is known that there is no universal method
for getting a strong consistent solution to this problem. Partial results for
Gaussian processes have been obtained in [33] and Schafer [43]. The results of
the latter have been extended for a wider class of Gaussian processes.
Recent results on control-Lyapunov-exponents of random matrix products have been applied to optimize logarithmic growth rate of currency portfolios under minimal conditions on the exchange rate matrix. The theory has been reaffirmed by simulation results, [31].
Hidden Markov
Models
(L. Gerencsér, I. Kmecs, Gy. Michaletzky, G. Molnár-Sáska, T. Szilágyi, Zs. Vágó)
Estimation of HMM-s : Hidden Markov Models
(HMM-s) are widely used due to their flexibility in modelling dynamical
phenomena in engineering, physics and economy. For the latter see [16], [18],
[36], [19]. A basic problem in the
theory of Hidden Markov Models is the estimation of the dynamics of the process. A tight connection between the estimation theory
of HMM-s and linear stochastic systems have been established in [2*], via the realization techniques of V. Borkar, [8] and the theory of L-mixing processes, [25]. As a
byproduct, conditions for non-linear stochastic systems are given under which
an L-mixing input generates an L-mixing output.
In establishing the above connection a key role is played by what is
called uniform exponential stability of the filter process ([1], [37]). The
results of [2*] have been extended to general compact state-space using the
results of [15]. These results have been applied to derive strong approximation
theorem for the estimates of HMM-parameters, [2*].
Another basic problem is to detect structural changes in the model. A change point detection method for HMMs has been inspired by the results of [26] and [2], leading a kind of Hinkley detector with appropriately defined residuals, [24]. An inflection in the on-line Hinkley statistics gives a clue for a change, see the figure below:
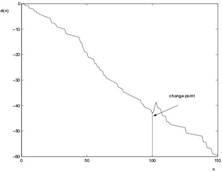
Quantized Gaussian linear models: We have investigated the identification of quantized Gaussian linear models. Our primary interest is in the estimation of quantized Gaussian ARMA-processes for speech restoration in mobile communication. This leads to integration in dimension 320 for a special MCMC (Markov Chain Monte Carlo) has been developed. The identifiability issue has been settled in [7*]. For static models, given by quantized linear regression, an effective real-time resursive estimation method, a randomized EM (Expectation Maximization) method has been developed and analyzed, [17].
Stochastic adaptive control and optimization
(L. Gerencsér,
S. Hill, Gy. Michaletzky,
Zs. Vágó)
Recursive
estimation : Risk sensitive estimation of
multivariable linear stochastic systems have been introduced and investigated.
This is a genuinely recursive estimation method with a weight matrix as a
design parameter. The optimal weight matrix has been determined using results
of stochastic realization theory, [4*]
More application to a basic result on the strong
approximation of recursive estimators leading to an exact characterization of
the loss in performance in stochastic adaptive control have been developed in [3*].
SPSA in discrete optimization. : The minimization of quadratic functions over the set of grid-points with integer coordinates is a basic problem in resource allocation fo r network design. We have further improved an MCMC (Markov-Chain Monte-Carlo) method in whic the initial Markoc chain is generated by the SPSA (simultaneous perturbation stochastic approximation) method by a careful choice truncations, averaging and acceptance probabilities ([29], [30], [1*]).
REFERENCES:
[1] ARAPOSTHTATIS, A.
– MARCUS, S. I.: Analysis of an Identification Algorithm Arising in the
Adaptive Estimation of Markov Chains, Math. of
Control, Signals and Systems, vol. 3, pp.1-29, 1990.
[2] BAIKOVICIUS, J. - GERENCSÉR, L.: Change point detection in a stochastic complexity framework. In: Proceedings of the 29-th IEEE CDC, vol. 6, pp. 3554-3555, 1990.
[3]
BAILEY, D. H.: Sequential Schemes for Classifying and Predicting Ergodic
Processes. Ph. D. Thesis,
[4] BENVENISTE, A. –
MÉTIVIER, M. - PRIOURET, P.: Adaptive Algorithms and Stochastic Approximations.
Springer Verlag,
[5] BERKES, I., - HORVÁTH, L., - KOKOSZKA,
P.S.: GARCH processes: structure and estimation. Bernoulli, vol.
9, pp. 201-207, 2003.
[6] BERKES, I., HORVÁTH, L., KOKOSZKA, P.S.: Testing for parameter constancy in GARCH(p,q) models. Statistics and Probability Letters, forthcoming.
[7] BERLINGER, E. - GERENCSÉR, L. - MÁTYÁS, Z. – RÁSONYI, M.: Analysis of an income contingent student loan system, manuscript, 2004.
[8] BORKAR, V. S.: On white noise representations in stochastic realization theory. SIAM J. Control Optim., vol. 31, pp.1093--1102, 1993.
[9] BOLLA, M. – MOLNÁR-SÁSKA, G.: Optimization problems for weighted graphs and related
correlation estimates. Discrete Mathematics, vol. 282, no. 1-3, pp. 23-33., 2004.
[10] BOLLERSLEV, T.: Generalized autoregressive conditional heteroscedasticity. Journal of Econometrics 31, pp. 307-327, 1986.
[11] Budapest Stock
Exchange, http://www.bet.hu/onlinesz/index.html.
[12] CHRISTENSEN, B.S.: Dynamic Programming, Multivariate GARCH models, and Futures Hedging. In: Proceedings of the International Conference on Stochastic Finance, Lisbon, Portugal, September 26-30, 2004, (electronic).
[13] COVER, T. M.: An algorithm for maximizing expected log investment return. IEEE Trans. on Information Theory, vol. 30, no. 2, part 2, pp. 369—373, 1984.
[14] COVER, T. M.: Open problems in information theory. In: Proceedings of the 1975 IEEE Joint Workshop on Information Theory, “IEEE Press”, New York, pp. 35-36, 1975.
[15] DOUC, R. – MATIAS, C.: Asymptotics of the Maximum likelihood estimator
for general Hidden Markov Models. Bernoulli, vol. 7,
pp. 381-420, 2001.
[16] ELLIOTT R. - VAN DER HOEK, J.: An application of hidden Markov models to asset allocation problems. Finance and Stochastics, vol. 1, no. 3, pp. 229-238,1997.
[17] FINESSO, L. - GERENCSÉR, L. – KMECS, I.-SZILÁGYI, T.: Estimation of quantized Gaussian linear models - a randomized EM method. Int. Journal of Adaptive Control and Signal Processing Control, submitted.
[18] FUH, C.D. – HU, I. – LIN, S.K.: Empirical performance and asset pricing in hidden Markov models. Comm. Statist. Theory Methods, vol. 32 , no. 12, pp. 2477-2512, 2003.
[19] GENON–CATALOT, V. – JEANTHEAU, T. – LAREDO, C.: Stochastic volatility models as hidden Markov models and statistical applications. Bernoulli, vol.6, no. 6, pp. 1051—1079, 2000.
[20] GERENCSÉR, L. – MÁTYÁS, Z - MOLNÁR-SÁSKA, G. - ORLOVITS, ZS..: Statistical theory of non-linear stochastic systems. I. www.sztaki.hu/~gerencs/download/BMP.ps
[21] GERENCSÉR, L. – MÁTYÁS, Z.: A behavioral stock market model. In: Proceedings of the International Conference on Stochastic Finance, Lisbon, Portugal, September 26-30, 2004, (electronic).
[22] GERENCSÉR, L. – MÁTYÁS, Z.: A system theoretic approach to behavioral finance. In: Proceedings of the 43rd IEEE Conference on Decision and Control, Nassau, The Bahamas, December 14-17, 2004, TuA10.2.
[23] GERENCSÉR, L. – MOLNÁR-SÁSKA, G. – ORLOVITS, Zs.: Change-detection of Hidden Markov Models and GARCH processes. In: Proceedings of the International Conference on Stochastic Finance, Lisbon, Portugal, September 26-30, 2004, (electronic).
[24] GERENCSÉR, L. – MOLNÁR-SÁSKA, G.: Change detection of
Hidden Markov Models. In: Proceedings of the 43rd
IEEE Conference on Decision and Control, Nassau, The Bahamas, December
14-17, WeA11.2, 2004.
[25] GERENCSÉR, L.: On a class of Mixing Processes. Stochastics, vol. 26, pp. 165-191, 1989.
[26] GERENCSÉR, L.: Predictive stochastic complexity associated with fixed gain esstimators. In: C. Praagman, J.W. Niueuwenhuis and H.L. Trentelman, (editors), Proceedings of the 2nd European Control Conference, Groningen, pp. 1673-1677, 1993.
[27] GERENCSÉR, L.: On the Martingale approximation of the estimation error of ARMA parameters. System & Control Letters, vol. 15, pp. 417-423, 1990.
[28] GERENCSÉR, L.: Fixed gain off-line
estimators of ARMA parameters. Journal of Mathematical Systems,
Estimation and Control, vol. 4, no. 2, pp. 249-252.
[29] GERENCSÉR, L. – HILL, S.D. - VÁGÓ, Zs. – VINCZE, Z.: Discrete optimization, SPSA and Markov Chain Monte Carlo methods. In: Proceedings of the American Control Conference 2004, June 30 - July 2, 2004, Boston, MA, USA, ThP17, pp. 3814-3819.
[30] HILL,S. D. – GERENCSÉR,L. -
VÁGÓ,Zs.: Stochastic Approximation on Discrete Sets Using Simultaneous
Perturbation Difference Approximations. In: Proceedings
of theAmerican Control
Conference 2004, June 30- July
2, 2004, Boston, MA, USA, ThM06, pp. 2795-2798.
[31] GERENCSÉR,L. – RÁSONYI, M.-VÁGÓ,Zs.:
Controlled Lyapunov-Exponents with Applications. In: Proceedings of the 43rd
IEEE Conference on Decision and Control, Nassau, The Bahamas, December
14-17, WeC08, 2004.
[32] GOMBAY, E.: Sequential change point detection
and estiamtion. Sequential Analysis 22, pp. 203-222, 2003.
[33] GYÖRFI, L. – LUGOSI, G.:
Strategies for sequential prediction of stationary time series, In: Dror, M. – L’Ecuyer, P. – Szidarovszky, M.(editors): Modeling
Uncertainity: An Examination of Stochastic Theory,
Methods, and Applications. Kluwer Academic Publishers,
pp. 225-248, 2002.
[34] HELMBOLD, D. P. –
SCHAPIRE, R. E. – SINGER, Y. – WARMUTH, M. K.: On-Line Portfolio Selection
Using Multiplicative Updates, Mathematical Finance, vol. 8, pp. 325-347,
1998.
[35] KAHNEMANN, D. - TVERSKY, A.: Rational Choice and the Framing of Decisions. Journal of Business,Vol. 59, pp. 251-278, 1986.
[36] LANDEN, C.: Bond pricing in a hidden Markov model of the short rate. Finance and Stochastics, vol. 4, no. 4, pp. 371-389, 2000.
[37] LEGLAND, F. – MEVEL, L: Exponential Forgetting and Geometric Ergodicity in Hidden Markov Models. Mathematics of Control, Signals and Systems, vol. 13, pp. 63-93, 2000.
[38] MAMMADLI, S.: Analysis of stock return and volatility using GARCH models: the case of Turkey. In: Proceedings of the International Conference on Stochastic Finance, Lisbon, Portugal, September 26-30, 2004, (electronic).
[39] RÁSONYI, M.: Utility maximization in discrete-time financial market models. In: Proceedings of the International Conference on Stochastic Finance, Lisbon, Portugal, September 26-30, 2004, (electronic).
[40] RÁSONYI, M.:
Arbitrage theory and risk-neutral measures. Decisions in
Economics and Finance, vol. 27, no. 2, pp. 109-123, 2004.
[41] RYABKO, B. YA.:
Prediction of random sequences and universal coding. Problems
of Information Transmission (Problemy Peredachi Informatsii), vol. 24, no.
2, pp. 3-14, 1988.
[42] SCHAFER, D.: Nonparametric Estimation for Financial Investment under Log-Utility. Ph.D. thesis, Mathematisches Institut A der Universitat Stuttgart, 2002.
[43] SCHAFER, D.:
Strongly consistent online forecasting of centered Gaussian processes. IEEE
Trans. on Information Theory, vol 48, no. 3, pp. 791-799, 2002.
[44] TERDIK, GY.: Bilinear Stochastic Models and Related Problems of Nonlinear Time Series Analysis. Lecture Notes in Statistics, Springer Verlag, New York, 1990.
PUBLICATIONS TO APPEAR:
[1*] HILL, S. D. – GERENCSÉR. L. - VÁGÓ, Zs.:
Discrete Stochastic Approximation via Simultaneous
Difference Approximation. American
Control Conference 2005, June
8 – June 10,
[2*] GERENCSÉR, L. – MICHALETZKY, GY. – MOLNÁR-SÁSKA, G. –
TUSNÁDY, G.: A new approach for the statistical analysis of Hidden Markov
Models. IEEE Trans. Automatic Control, under revision
[3*] GERENCSÉR, L.: A representation theorem for recursive estimators. SIAM Journal on Control and Optimization. Accepted for publication.
[4*] GERENCSÉR, L. - MICHALETZKY, Gy. - VÁGÓ, Zs.: Risk-sensitive identification of linear stochastic systems. Mathematics of Control, Signals and Systems. Accepted for publication.
[5*] RÁSONYI,M.
– STETTNER, L.: On utility maximization in discrete-time market models. Annals
of Applied Probability, Accepted for publication.
[6*] RÁSONYI, M.: Arbitrage on large
financial markets (in Hungarian). SIGMA, accepted for
publication.
[7*] SZEIDL, Á. – GERENCSÉR, L. –
MICHALETZKY, GY.: Quantized Gaussian ARMA
identification. Systems and Control Letters, accepted for publication.
GRANTS, AWARDS
Project title: Stochastic
Systems and Modelling Financial Markets
Hungarian National Science Foundation (OTKA)
Supervisor: L. Gerencsér
OTKA grant No.: T047193
Duration: 2002-2006
APPENDIX 1
EDUCATIONAL ACTIVITIES
a. Graduate
courses
Gerencsér, L.:
Péter Pázmány Catholic University,
Faculty of Information Technology,
Budapest,
Information and coding theory (lecturer)
2003/2004/I.
Mátyás, Z. :
Péter Pázmány Catholic University,
Faculty of Information Technology,
Probability theory and statistics (TA),
2004/2005/I.
Molnár-Sáska,
G.:
Budapest University of Technology and Economics,
Institute of Mathematics,
Seminar on applied mathematics
2004/05/I
Statistics
2004/05/I
Central European University,
Department of Computer Sciences,
Statistics (lecturer)
2003/2004 /II
Péter Pázmány Catholic University,
Faculty of Information Technology,
Probability theory and statistics (TA)
2004/05/I
Orlovits, Zs.:
Péter Pázmány Catholic University,
Faculty of Information Technology,
Budapest,
Analysis (TA)
2004/2005/I
Rásonyi, M.:
Péter Pázmány Catholic University,
Faculty of Information Technology,
Budapest,
Stochastic processes
2004/2005/I
Probability theory and statistics (lecturer)
2004/2005/II
b. Postgraduate
courses
Gerencsér, L.:
Eötvös Loránd University
Faculty of Natural
Sciences,
Budapest
Statistical theory of non-linear stochastic systems, I. (seminar)
2003/2004/II.
Eötvös Loránd University
Faculty of Natural
Sciences,
Budapest
Statistical theory of non-linear stochastic systems, II. (seminar)
2004/2005/I.
c. Ph.D.
students
Molnár-Sáska, G.: Hidden Markov processes in financial modelling (1999-)
Budapest University of Technology and Economics
“Computer Science” Ph.D. program
Supervisors: M. Bolla
and L. Gerencsér
Mátyás, Z.: Behaviour
models of financial markets (2002-)
Eötvös Loránd University, Budapest, Faculty of Natural Sciences,
“Applied Mathematics” Ph.D. program
Supervisor: L. Gerencsér
Orlovits, Zs.: Statistical estimation of economic time series. (2003-)
Eötvös Loránd University, Budapest, Faculty of Natural Sciences,
“Applied Mathematics” Ph.D. program
Supervisor: L. Gerencsér
APPENDIX 2.
SCIENTIFIC AND
OTHER ACTIVITIES
International
activities
Editorial
IEEE Transactions
on Automatic Control, (L. Gerencsér, 2001-2004)
SIAM J. Control and Optimization (L. Gerencsér, 1998-2004)
Conference
organization:
International Program
Committee for the 2005 joint CDC-ECC (L. Gerencsér)
ERNSI (European Research Network on System Identification) Workshop on System Identification 2004, Dobogókő, October 4-6, 2004. Local chairman (L. Gerencsér).
Memberships (L. Gerencsér)
ERCIM Working Group on Control and Systems,
chairman (L. Gerencsér).
ERNSI (European Network for System Identification), 2003-
IEEE Control Systems Society Committee for International Affairs
Vice Chair of the IFAC Techical Committe on Stochastic Systems
Local activity
L. Gerencsér is an associate editor for the Journal on Applied Mathematics (Alkalmazott Matematikai Lapok).
L. Gerencsér
is a member of the Committee for Operations Research of the
G. Molnár-Sáska is the secretary of the Seminar for
Applied Mathematics, Budapest University of Technology and Economics, Faculty
of Science.
Education
Z. Mátyás has received the degree of "Teacher of mathematics" at the Eötvös Loránd University, Budapest, Faculty of Natural Sciences (2000-2004).
Z. Mátyás finished his fourth year of study at the University of Economic Sciences and Public Administration, (2000-).